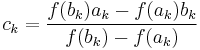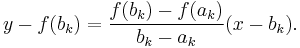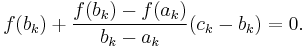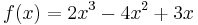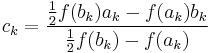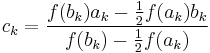False position method
The false position method or regula falsi method is a term for problem-solving methods in algebra and calculus. In simple terms, these methods begin by attempting to evaluate a problem using test ("false") values for the variables, and then adjust the values accordingly.
Contents |
Algebra
In algebra, the false position method or regula falsi method same term is used to refer to basic trial and error methods of solving equations, by substituting test values for the variables in an equation. This is sometimes also referred to as "guess and check". Versions of this methods predate standard algebraic methods for factoring polynomials, and can be found in ancient Egyptian and Indian mathematics.
The oldest surviving document demonstrating knowledge and proficiency in the false position method is the Indian mathematical text Vaishali Ganit (c. 3rd century BC). The ancient Chinese mathematical text called The Nine Chapters on the Mathematical Art (九章算術) dated from 200 BC to AD 100 also mentions the algorithm. Between the 9th and 10th centuries, Islamic mathematician Abu Kamil wrote a now lost treatise on the use of double false position, known as the Book of the Two Errors (Kitāb al-khaṭaʾayn).[1] Leonardo of Pisa (Fibonacci) mentions false position in his book Liber Abaci published in AD 1202, following the method that he learned from Arab sources.
Numerical Analysis
In numerical analysis, the false position method is a root-finding algorithm that combines features from the bisection method and the secant method.
Like the bisection method, the false position method starts with two points a0 and b0 such that f(a0) and f(b0) are of opposite signs, which implies by the intermediate value theorem that the function f has a root in the interval [a0, b0], assuming continuity of the function f. The method proceeds by producing a sequence of shrinking intervals [ak, bk] that all contain a root of f.
At iteration number k, the number
is computed. As explained below, ck is the root of the secant line through (ak, f(ak)) and (bk, f(bk)). If f(ak) and f(ck) have the same sign, then we set ak+1 = ck and bk+1 = bk, otherwise we set ak+1 = ak and bk+1 = ck. This process is repeated until the root is approximated sufficiently well.
The above formula is also used in the secant method, but the secant method always retains the last two computed points, while the false position method retains two points which certainly bracket a root. On the other hand, the only difference between the false position method and the bisection method is that the latter uses ck = (ak + bk) / 2.
Finding the root of the secant
Given ak and bk, we construct the line through the points (ak, f(ak)) and (bk, f(bk)), as demonstrated in the picture on the right. Note that this line is a secant or chord of the graph of the function f. In point-slope form, it can be defined as
We now choose ck to be the root of this line (substituting for x), and setting  and see that
and see that
Solving this equation gives the above equation for ck.
Analysis
If the initial end-points a0 and b0 are chosen such that f(a0) and f(b0) are of opposite signs, then one of the end-points will converge to a root of f. Asymptotically, the other end-point will remain fixed for all subsequent iterations while the converging endpoint becomes updated. As a result, unlike the bisection method, the width of the bracket does not tend to zero. As a consequence, the linear approximation to f(x), which is used to pick the false position, does not improve in its quality.
One example of this phenomenon is the function
on the initial bracket [−1,1]. The left end, −1, is never replaced and thus the width of the bracket never falls below 1. Hence, the right endpoint approaches 0 at a linear rate (with a rate of convergence of 2/3).
Illinois algorithm
While it is a misunderstanding to think that the method of false position is a good method, it is equally a mistake to think that it is unsalvageable. The failure mode is easy to detect (the same end-point is retained twice in a row) and easily remedied by next picking a modified false position, such as
or
down-weighting one of the endpoint values to force the next ck to occur on that side of the function. The factor of 2 above looks like a hack, but it guarantees superlinear convergence (asymptotically, the algorithm will perform two regular steps after any modified step). There are other ways to pick the rescaling which give even better superlinear convergence rates.
The above adjustment, and other similar modifications to Regula Falsi are called the Illinois algorithm. Ford (1995) summarizes and analyzes the superlinear variants of the modified method of false position. Judging from the bibliography, modified regula falsi methods were well known in the 1970s and have been subsequently forgotten or misremembered in current textbooks.
Example code
C code was written for clarity instead of efficiency. It was designed to solve the same problem as solved by the Newton's method and secant method code: to find the positive number x where cos(x) = x3. This problem is transformed into a root-finding problem of the form f(x) = cos(x) - x3 = 0.
#include <stdio.h> #include <math.h> double f(double x) { return cos(x) - x*x*x; } double FalsiMethod(double s, double t, double e, int m) { int n,side=0; double r,fr,fs = f(s),ft = f(t); for (n = 1; n <= m; n++) { r = (fs*t - ft*s) / (fs - ft); if (fabs(t-s) < e*fabs(t+s)) break; fr = f(r); if (fr * ft > 0) { t = r; ft = fr; if (side==-1) fs /= 2; side = -1; } else if (fs * fr > 0) { s = r; fs = fr; if (side==+1) ft /= 2; side = +1; } else break; } return r; } int main(void) { printf("%0.15f\n", FalsiMethod(0, 1, 5E-15, 100)); return 0; }
After running this code, the final answer is approximately 0.865474033101614
See also
- Ridders' method, another root-finding method based on the false position method
- Brent's method
- Secant method
Notes
- ^ Schwartz, R. K (2004). "Issues in the Origin and Development of Hisab al-Khata’ayn (Calculation by Double False Position)". Eighth North African Meeting on the History of Arab Mathematics. Radès, Tunisia.
References
- J.A. Ford (1995). Improved Algorithms of Illinois-type for the Numerical Solution of Nonlinear Equations. Technical Report CSM-257. University of Essex Press.
- Richard L. Burden, J. Douglas Faires (2000). Numerical Analysis, 7th ed. Brooks/Cole. ISBN 0-534-38216-9.
- L.E. Sigler (2002). Fibonacci's Liber Abaci, Leonardo Pisano's Book of Calculation. Springer-Verlag, New York. ISBN 0-387-40737-5.